Fenómenos de interferencia y birrefringencia

POSICIONES DE EXTINCIÓN E ILUMINACIÓN
Los colores que se producen en el microscopio petrográfico, al colocar el segundo polarizador, están ocasionados por fenómenos de interferencia de la luz polarizada con los medios anisótropos. En los medios isótropos no se producen estos procesos de interferencia, por lo que, entre polarizadores cruzados, y para cualquier posición, siempre se observan en extinción (de color negro).
Al estudiar un mineral anisótropo entre polarizadores cruzados, observamos una variación máxima de los colores en un giro de 45º, entre la posición de menor iluminación (posición de extinción) y el color de interferencia (posición de máxima iluminación). Cuando el mineral presenta la mínima iluminación (normalmente oscuridad completa) decimos que está en extinción. En estas posiciones no se produce la doble refracción y solo se transmite un haz de luz polarizada cuyo plano de polarización coincide con el del polarizador del microscopio y se anula en el analizador (ver figura, casos 1 y 2). En el resto de posiciones (iluminadas) se produce una doble refracción, de forma que la muestra es atravesada por dos rayos de luz polarizada con planos de vibración perpendiculares entre sí.
En los casos mostrados en la figura (casos 3, 4 y 5) los vectores azules (orientados este-oeste) representan la luz polarizada incidente que coincide con la posición del polarizador del microscopio. Este rayo se desdobla en dos rayos polarizados perpendiculares entre sí que coinciden con las direcciones de vibración preferentes del cristal (vectores anaranjados y verdes). La amplitud relativa, de la que depende la intensidad de cada rayo, varía con el ángulo de giro. En todos los casos (esquemas centrales de los casos 1 a 5) la intensidad de la luz que emerge del cristal es la misma, exceptuando los minerales pleocroicos (ver Raith et al., 2012). En los esquemas de la derecha se muestran (vectores rojos) los componentes note-sur, obtenidos por descomposición vectorial, que coinciden con la dirección preferente del segundo polarizador y son capaces de atravesarlo, de manera que la máxima iluminación se da cuando el mineral está girado 45º desde su posición de extinción (caso 5). Como la luz utilizada, en el microscopio, es blanca, y por lo tanto policromática, el color de interferencia depende de las proporciones, de cada una de las diferentes longitudes de onda, que atraviesan este segundo polarizador (fenómenos de interferencia).
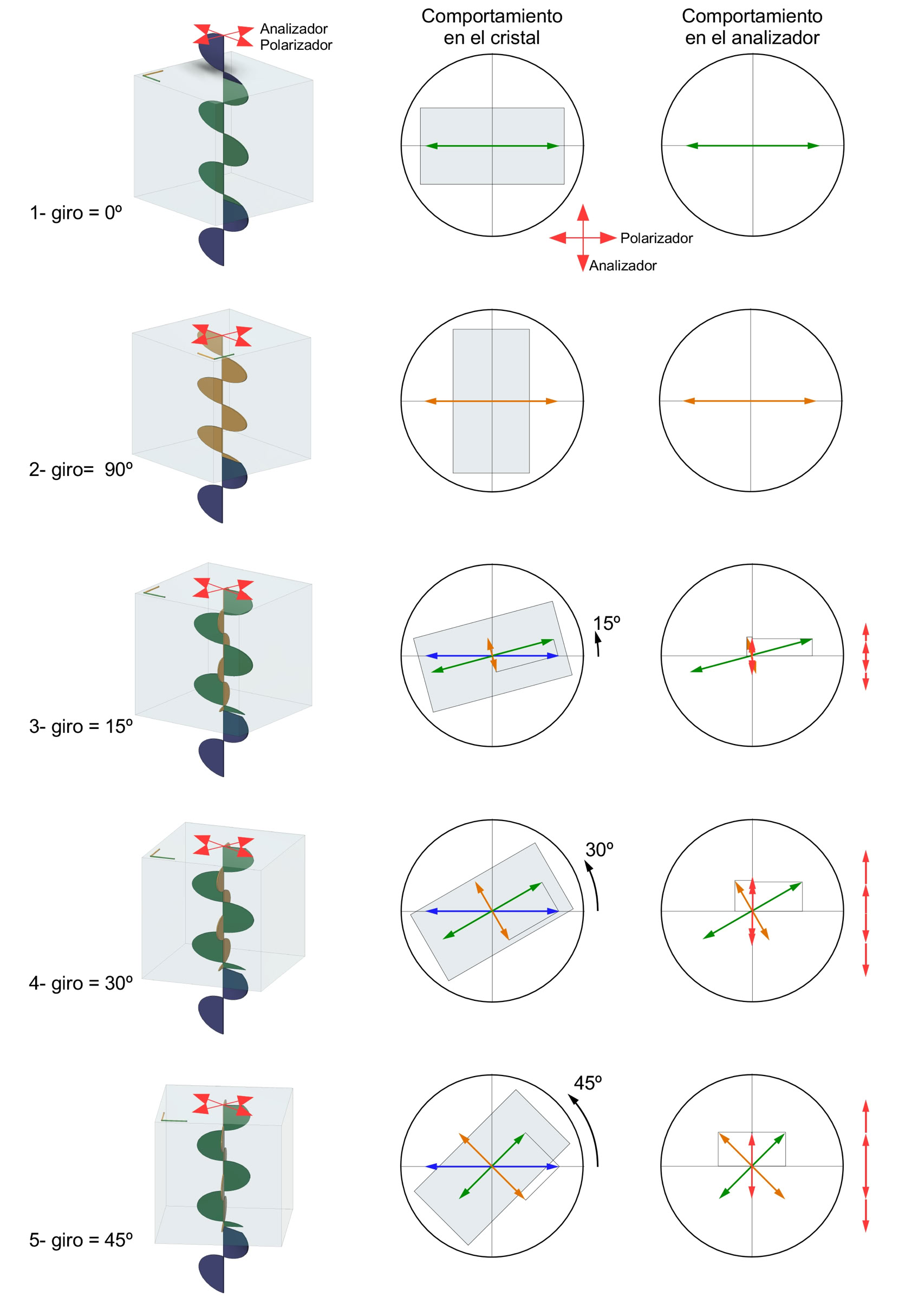
Izquierda: posiciones de extinción (1 y 2) y desdoblamiento en dos rayos polarizados en posiciones de iluminación (3 a 5). Centro: variación de las amplitudes relativas de los dos rayos polarizados con el giro. Derecha: descomposición vectorial de las amplitudes mostrando la intensidad de la luz que puede atravesar el segundo polarizador (máxima a 45º de la posición de extinción).
BIRREFRINGENCIA
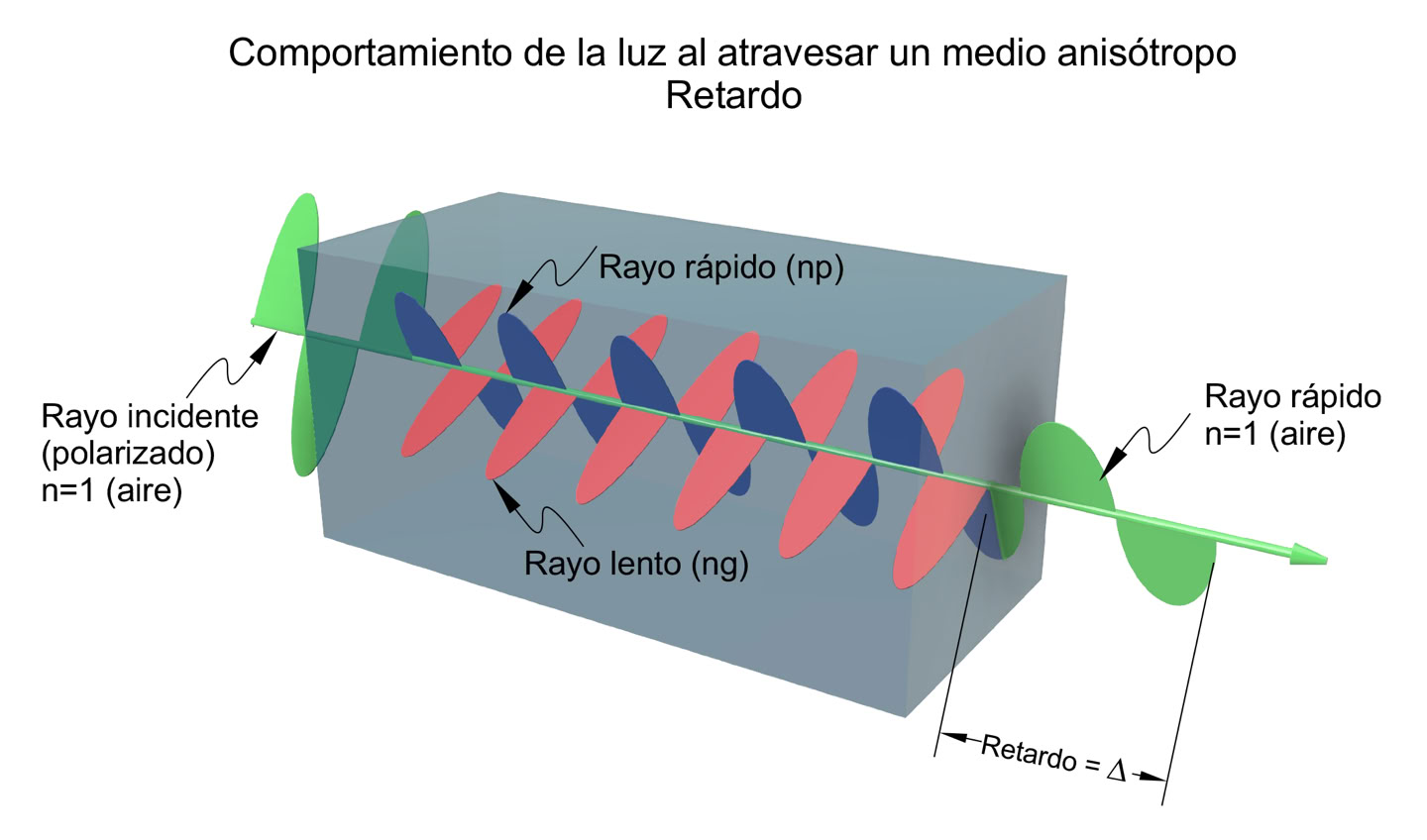
Las velocidades de los dos rayos polarizados son diferentes ya que tienen diferentes índices de refracción, el rayo de mayor índice de refracción (ng) es el más lento mientras que el de índice de refracción menor (np) es el más rápido. Definimos la birrefringencia, además de como la existencia de una doble refracción de los medios anisótropos, como el valor de la diferencia entre los índices de refracción de un medio anisótropo (ng-np).
Durante el tiempo que el rayo lento atraviesa el medio anisótropo el rápido ha conseguido una ventaja sobre el lento que se denomina retardo (Δ). Una vez que los dos rayos polarizados han atravesado el medio anisótropo mantienen el retardo y continúan como dos rayos perpendicularmente polarizados que vuelven a transmitirse a la misma velocidad. La relación entre el retardo (Δ), el espesor del mineral (d) y la birrefringencia (ng-np) viene dada por la relación:
Δ = d (ng - np)
Retardo, el esquema muestra el momento en que el rayo lento, de mayor índice de refracción (en rojo), atraviesa el mineral anisótropo. El retardo es la diferencia de recorrido entre el rayo rápido (np) y el lento (ng), o lo que es lo mismo, la ventaja que saca el rayo rápido al lento durante el tiempo que tarda el rayo lento en atravesar el mineral.
FENOMENOS DE INTEREFERENCIA
Para comprender cómo se generan los colores de interferencia es necesario conocer los conceptos de interferencia (constructiva o destructiva) que se producen cuando los dos rayos de luz polarizada alcanzan el segundo polarizador.
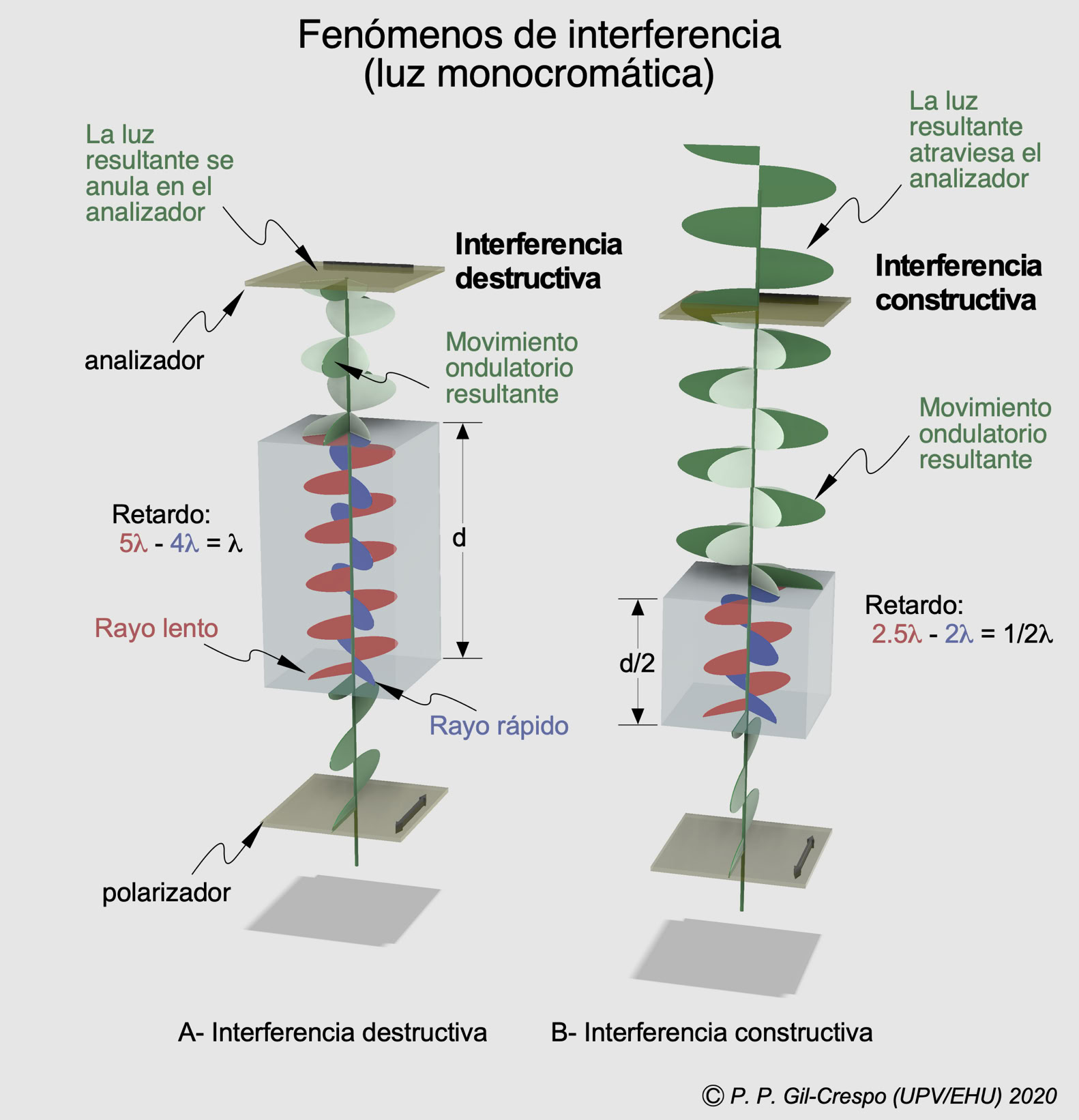
Si consideramos un rayo de luz monocromática (de λ = cte.) que atraviesa un medio anisótropo, los dos rayos polarizados alcanzan el segundo polarizador y pueden dar lugar a interferencias destructivas o constructivas con dos posibilidades extremas (ver figura):
- Interferencia destructiva (ejemplo A en la figura): En el caso de que el retardo = nλ (un múltiplo entero de la longitud de onda de la luz), el movimiento ondulatorio resultante de los dos rayos polarizados es perpendicular a la dirección preferente del analizador, se anulará en este y la transmisión de luz será nula.
- Interferencia constructiva (ejemplo B en la figura).: Si el retardo = ½ +nλ, el rayo resultante será paralelo al plano preferente del analizador, por lo que podrá atravesarlo dando lugar a un máximo de transmisión.
- Entre estos dos extremos tenemos posibilidades de interferencia con intensidades de transmisión intermedias.
Luz monocromática, fenómenos de interferencia. A) Interferencia destructiva (sin transmisión de luz en el analizador); B) Interferencia constructiva (máxima transmisión en el analizador).
COLORES DE INTERFERENCIA Y TABLA DE MICHEL-LÉVY
Para cada una de las componentes de la luz blanca, podemos representar las posiciones de los máximos y mínimos de transmisión, frente al retardo, que dependerán de las respectivas longitudes de onda (ver figura).
Como la luz utilizada, en el microscopio, es blanca, y por lo tanto policromática, para un retardo determinado, cada rayo de luz monocrómatico presenta un grado trasmisión diferente. Para un retardo determinado, el color de interferencia resultante dependerá de las proporciones de las diferentes longitudes de onda que pueden atravesar el segundo polarizador. El conjunto de todos los posibles colores de interferencia nos da como resultado la serie de colores establecida en la tabla de Michel-Lévy (ver figura). Por ejemplo, para un retardo de 400 nm no hay transmisión de la luz violeta (400) y muy baja para el azul (460), pero sí hay una transmisión importante de la luz correspondiente al rojo (700) y al anaranjado (620), por lo que el color de interferencia resultante es un naranja suave (ver tabla de Michel-Lévy).
Este fenómeno se puede comprobar fácilmente, utilizando filtros de luz monocromática en el sistema de iluminación del microscopio, al observar la figura de interferencia (en el ejemplo una figura uniáxica). Si utilizamos un filtro rojo (A) podemos ver cuatro máximos de transmisión (isocromas rojas) separados por tres zonas de transmisión igual a cero (isocromas oscuras). En el caso de utilizar una luz monocromática verde (B) observamos cinco máximos de transmisión (isocromas verdes) separados por cuatro de transmisión cero (isocromas oscuras). Con luz blanca (policromática) tenemos las isocromas correspondientes a los colores de la tabla de Michel Lévy (C) .
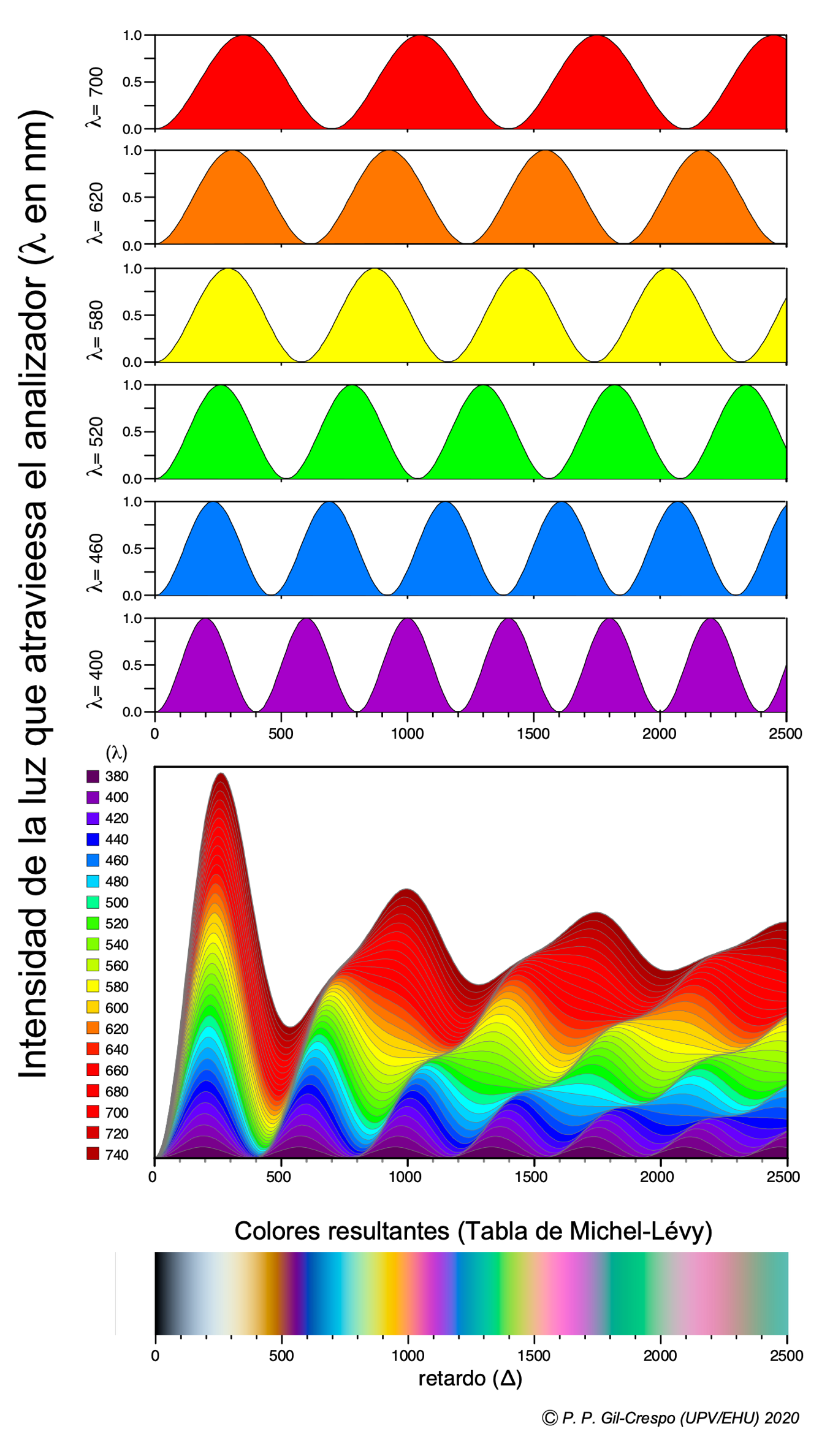
Arriba: diferencias de transmisión y absorción en el segundo polarizador, para las longitudes de onda de los colores básicos, en función de sus longitudes de onda y del retardo. Centro: distintas proporciones, de cada longitud de onda, que atraviesan el analizador para cada valor de retardo. Abajo: en la tabla de Michel-Lévy se ordenan todos los posibles colores de interferencia, originados por las distintas proporciones de cada longitud de onda que atraviesan el analizador.
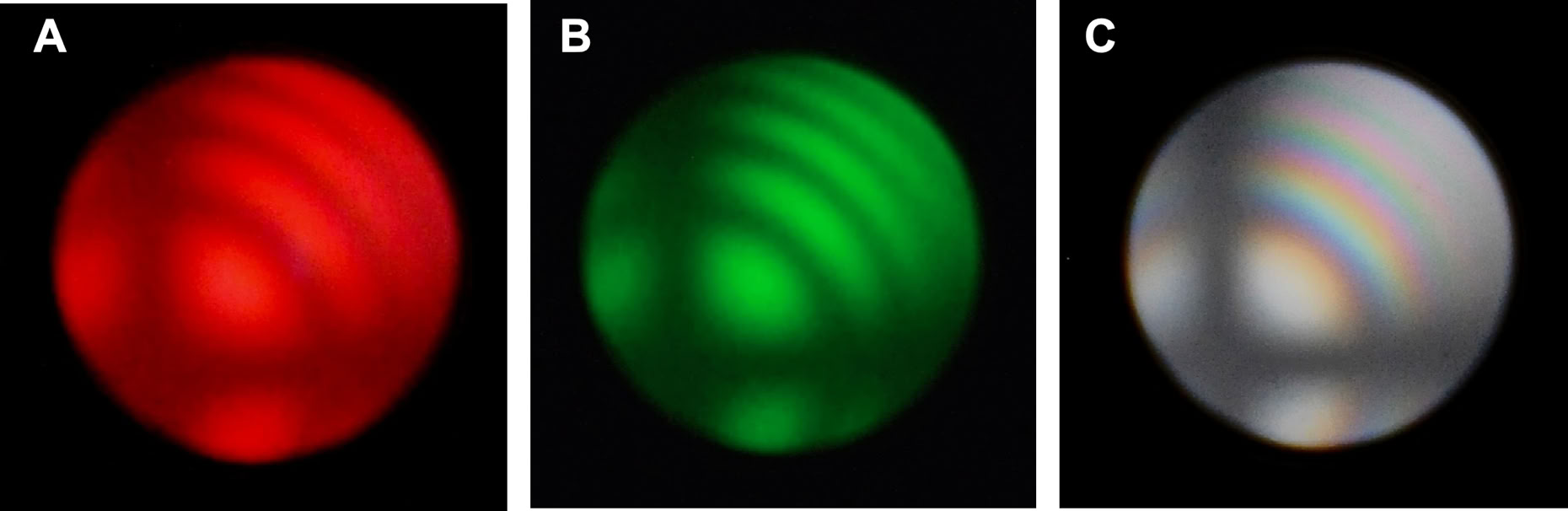
Figura de interferencia uniáxica observada utilizando diferentes tipos de luz : monocromática roja (A), monocromáitca verde (B) y luz blanca policromática (C).
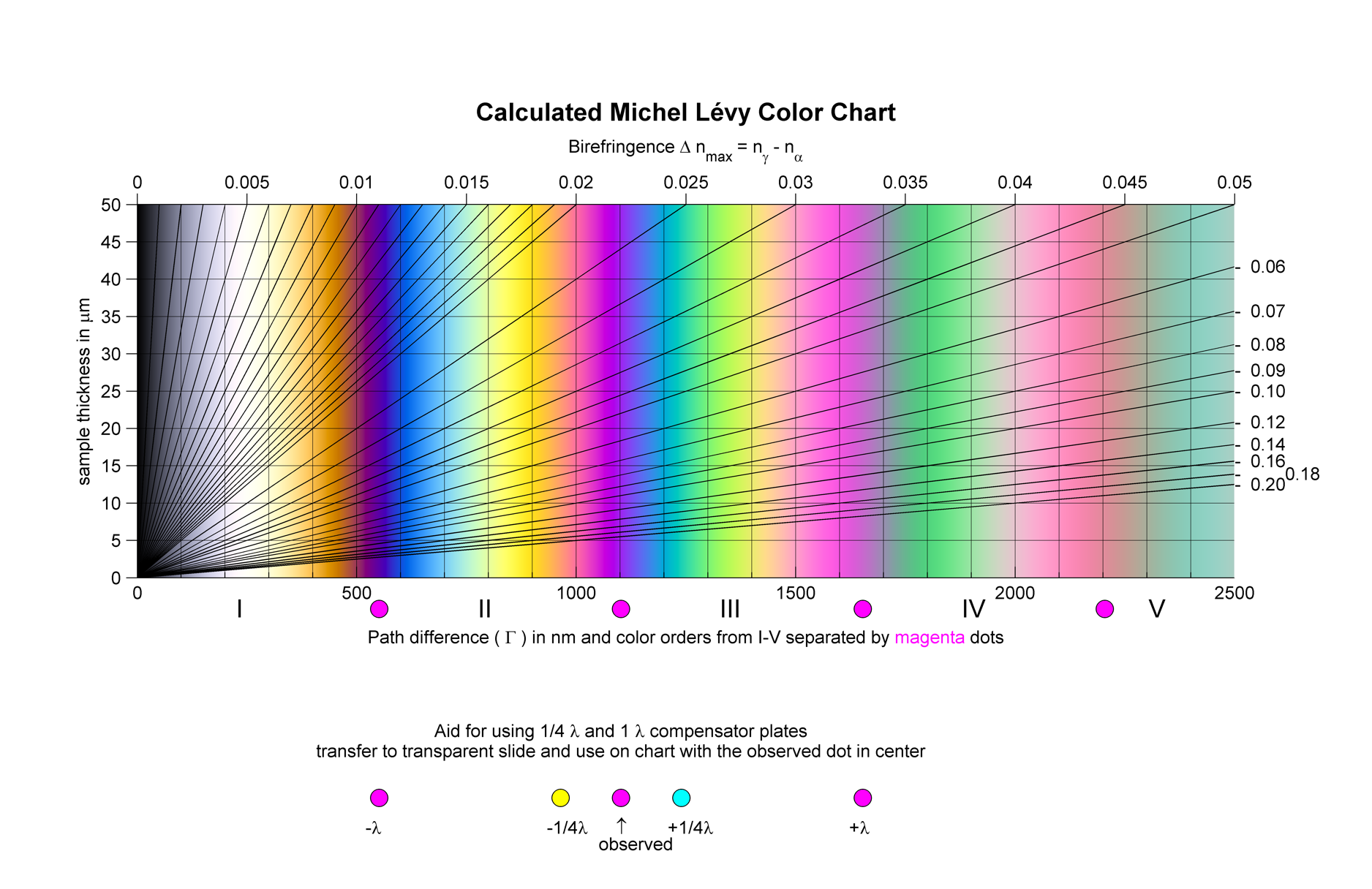
Tabla de Michel-Lévy (calculada). En el eje horizontal inferior se representa el retardo en nm, en el eje vertical izquierdo el espesor de la lámina delgada en micras y en los ejes horizontal superior y vertical derecho la birrefringencia (tomado de Sørensen, 2013).
DETERMINACIÓN DE LA BIRREFRINGENCIA
En una lámina delgada el color de interferencia para un grano determinado es un valor del retardo ya que su birrefringencia y el espesor (30 micras) son constantes, por lo que identificado el color de interferencia y teniendo en cuenta la ecuación, Δ= d (ng - np) podemos calcular la birrefringencia (ver figura). Como normalmente no conocemos los valores exactos del espesor de la lámina y del retardo, indicamos la birrefringencia de forma aproximada como: muy baja (<0,005), baja (0,005-0,012), media (0,012-0,025), alta (0,025-0,040), muy alta (0,040-0,080), o extrema (>0,080).
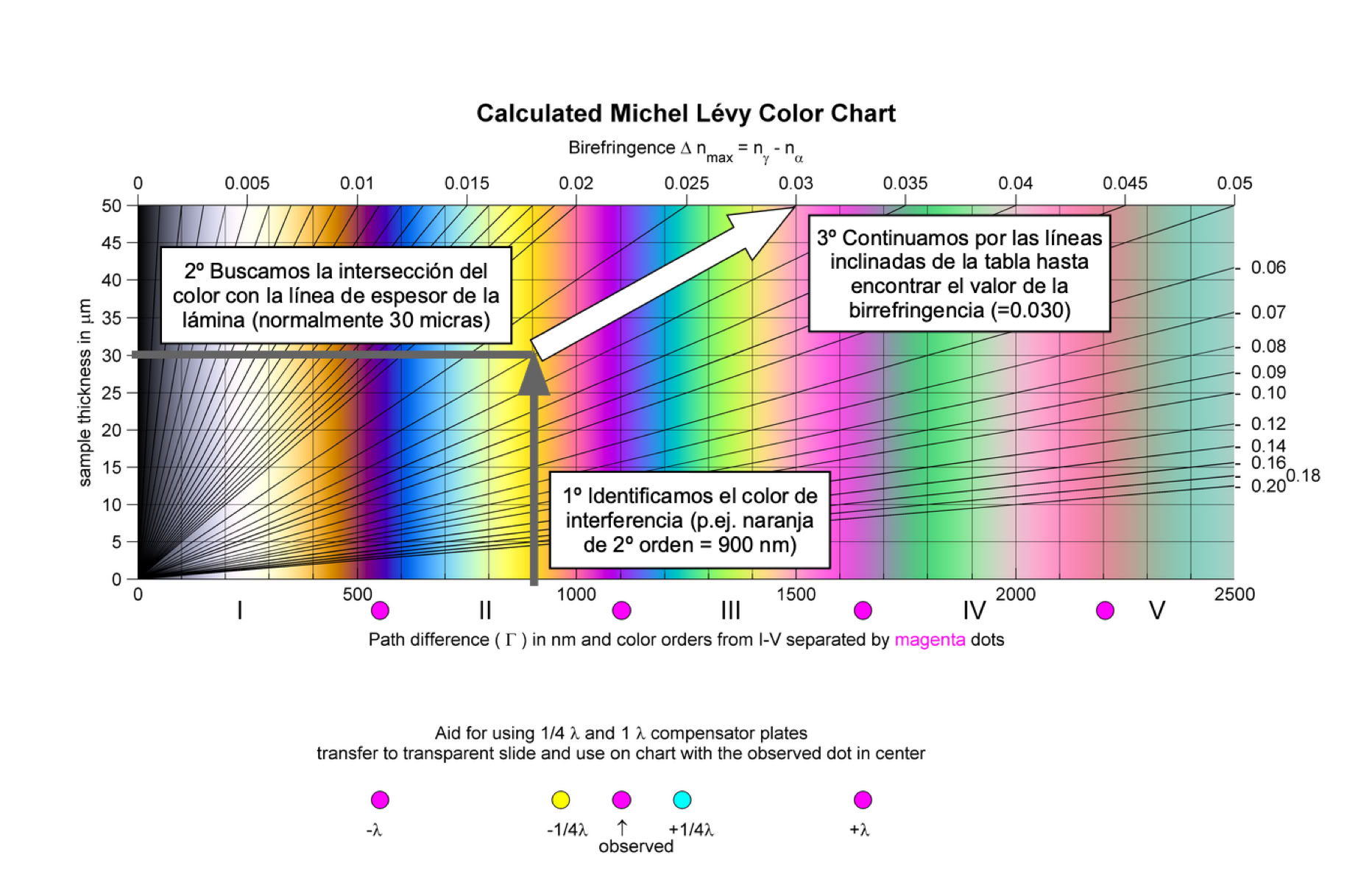
Pasos para la estimación de la birrefringencia en función del color interferencia mediante la tabla de Michel-Lévy (modificado de Sørensen, 2013).
Debemos de tener en cuenta que, por efecto de la anisotropía, las propiedades ópticas, y por tanto la birreftingrencia, varían en función de la sección concreta de cada uno de los diferentes granos del mismo mineral en una lámina delgada. El color de interferencia de un mineral puede variar, desde el negro (extinción) en una sección isótropa de birrefringencia=0 (en las secciones perpendiculares a un eje óptico), hasta un valor máximo (en las secciones paralelas al eje óptico, en los cristales uniáxicos, o a los dos ejes ópticos en los biáxicos). En los granos con secciones de birrefringencia máxima encontraremos el color que necesitamos identificar para, utilizando la tabla de Michel-Lévy, estimar la birrefringencia.
Cristales de diópsido, la variación en los colores de interferencia se debe a las diferentes orientaciones de las secciones de los cristales.
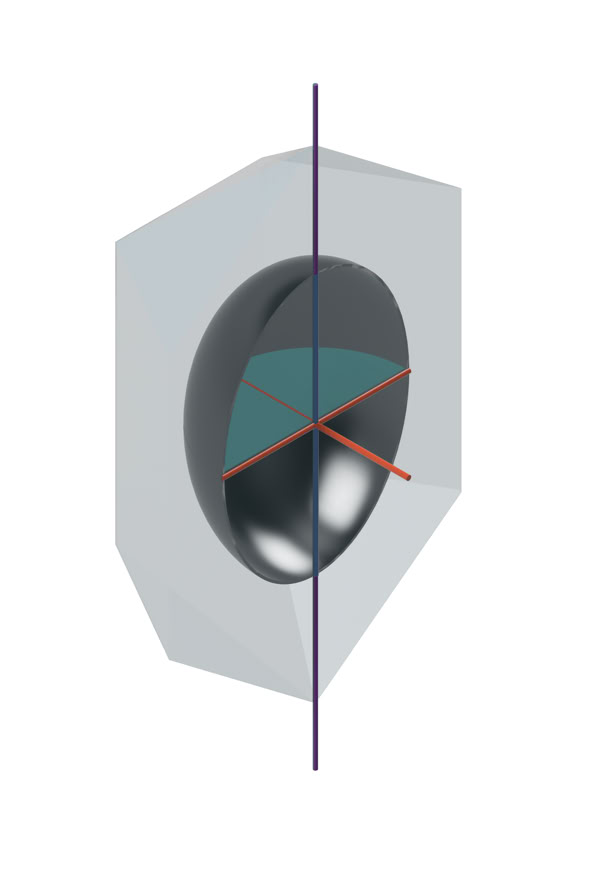
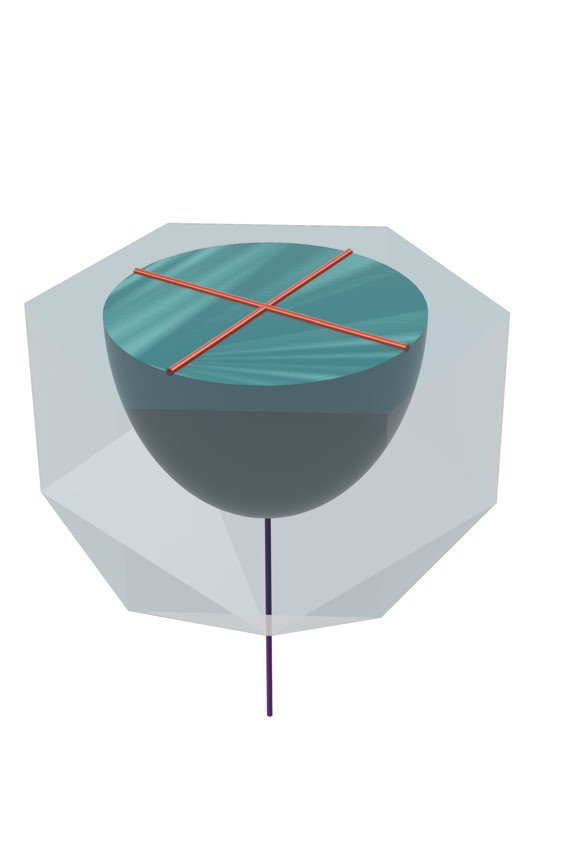
Modelos representando diferentes secciones de un cristal de cuarzo. Izquierda: sección longitudinal (paralela al eje óptico) de birrefringencia máxima. Centro: sección transversal (perpendicular al eje óptico) e isótropa. Derecha: sección cualquiera entre estas dos con birrefringencia intermedia. Los índices de refracción se representan en: azul claro, el correspondiente al rayo extraordinario (ε), en naranja el correspondiente al ordinario (ω), y los índices intermedios (ε’) en verde.
VISUALIZACIONES 3D: Los modelos 3D están generados con la aplicación Autodesk Fusion 360 (de la firma Autodesk). Permiten la visualización "on line" de los modelos en 3D, realizar giros y modificar distintas variables como el zoom, tipo de iluminación y otras (más fácil de manipular activando la opción pantalla completa).
Las diferentes posibilidades de secciones, en función del tipo de indicatriz óptica, se muestran en la tabla “Secciones de indicatrices“ (ver Anexos).
MÉTODOS DE IDENTIFICACIÓN DEL COLOR DE INTERFERENCIA
Para determinar la birrefringencia de un mineral debemos de conocer el retardo generado entre el rayo rápido y el rayo lento. Para ello necesitamos identificar el color de interferencia del mineral. A partir de este color y conociendo el espesor de la lámina delgada (normalmente 30µm), utilizamos la tabla de Michel-Lévy para estimar la birrefringencia.
Existen diferentes métodos para determinar el color de interferencia, como son la utilización de filtros como el compensador λ, que produce un retardo de 530nm, o la cuña de cuarzo que es un compensador que produce un retardo variable, en función de la zona de la cuña empleada. Con ambos dispositivos, el retardo se produce en el rayo que vibra perpendicularmente a la dirección de introducción del compensador (a 45º de la dirección N-S del microscopio), lo que nos permite identificar las posiciones del rayo rápido y del lento
IDENTIFICACIÓN DEL COLOR DE INTERFERENCIA UTILIZANDO EL COMPENSADOR λ (530nm)
Partimos de la posición de extinción del mineral, en la cual las dos direcciones de vibración preferentes coinciden con las direcciones de los polarizadores. Al girar un grano a 45º de la posición de extinción (ver Figura: A y B) tendremos uno de dos rayos polarizados colocado en la posición de retardo de los compensadores (a 45º del N-S del microscopio y el otro a 90º de este). Si, con el mineral en esta posición, introducimos el compensador λ, el rayo que vibra en la dirección de 45º se verá retardado en una cantidad igual a 530 nm, con los que el color de interferencia del grano variará. Tenemos dos posibilidades: a) que el rayo colocado en la posición de retardo sea el lento (el de indice de refracción mayor=ng) y, en este caso, al retardar al rayo lento aumentaremos el retardo total con lo que el color de interferencia subirá (ver Figura: A y C), b) si el color de interferencia baja (ver Figura: B y D) nos indica que estamos retardando al rayo más rápido (el de indice de refracción menor=np). Decimos que el color sube cuando el color de interferencia se desplaza a hacia colores de ordenes superiores (hacia la derecha de la tabla de Michel-Lévy) y baja cuando el desplazamiento es hacia órdenes inferiores (hacia la izquierda de la tabla).
En minerales con colores de interferencia de primer orden o del principio del segundo orden (birrefringencias bajas-medias), es posible identificar el color utilizando, solamente, el compensador λ. Si el color de bajada es gris o blanco (ver Figura: D) quiere decir que el color de interferencia, del mineral, es del final del primer orden o principio del segundo (ver Figura). Si el color de bajada es más alto (rojo, azul, verde, etc.) utilizaremos el método de la cuña de cuarzo. Una vez identificado el color de interferencia, la birrefringencia se calcula con la tabla de Michel-Lévy.
Al utilizar este método, si el color de interferencia del mineral es gris el color de subida será azul y el de bajada anaranjado. Aparentemente estos dos colores son más altos que el gris, pero el azul se obtiene al sumar 530 nm a un retardo de ~ 100nm (gris) dando lugar a un retardo total de 630 nm (azul). El color anaranjado, de bajada, se obtiene al restar 530nm a 100nm (obteniendo 430 nm, en valor absoluto).
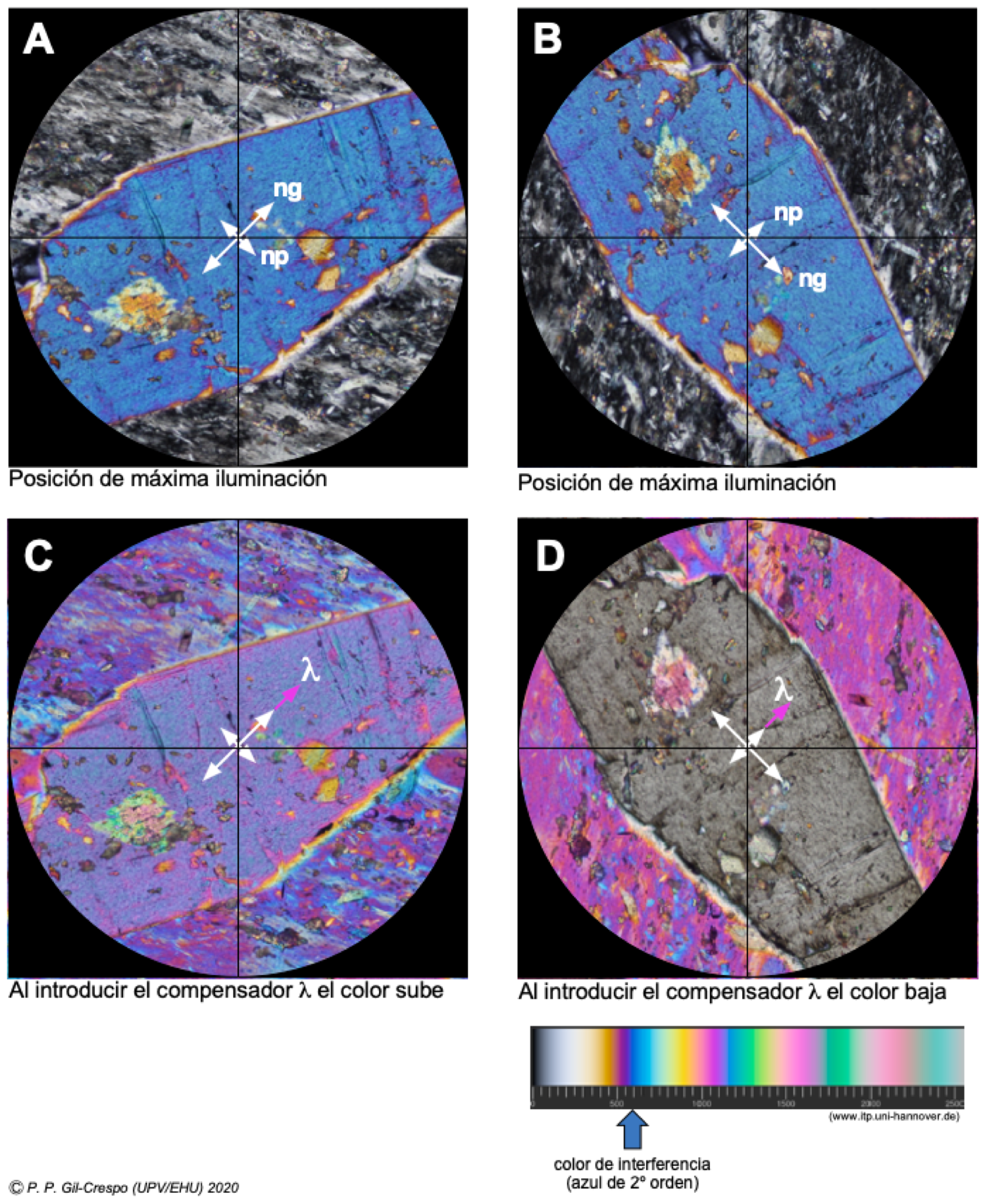
Identificación del color de interferencia utilizando el compensador λ (530nm). En A y en B tenemos las dos posiciones posibles de máxima iluminación (a 45º de la posición de extinción) mostrando el color de interferencia que queremos identificar. Necesitamos el mineral en la posición de bajada de color (D), por lo que si, al introducir el compensador λ, el color sube (C), giramos la platina del microscopio 90º (D). En esta posición, el color de bajada es gris (de primer orden), por lo que el color de interferencia corresponde al azul de 2º orden (530nm más alto que el gris).
IDENTIFICACIÓN DEL COLOR DE INTERFERENCIA MEDIANTE LA CUÑA DE CUARZO
La cuña de cuarzo es un prisma de cuarzo incoloro que funciona de manera similar al compensador λ pero que produce un retardo variable de hasta 6º orden y es útil para identificar colores de interferencia de 2º orden o superiores.
El primer paso (ver Fig. A) es colocar el grano en extinción, (de forma que los dos planos de vibración de luz coincidan con los ejes del retículo).
El siguiente paso es colocar el grano de forma que la cuña de cuarzo retarde al rayo más rápido, para ello giramos la platina 45º, para encontrar la posición de máxima iluminación (ver Fig. B), e introducimos el compensador λ en la ranura de accesorios. En el caso de que el color baje (ver Fig. C), estamos retardando al rayo rápido, y dejamos la platina en la misma posición. Si vemos que sube el color, quiere decir que estamos retardando al rayo más lento, por lo que giraremos otros 90º para obtener la posición bajada de color.
Una vez colocado el mineral en la posición de bajada de color, sacamos el compensador e introducimos, en su lugar, la cuña de cuarzo muy lentamente (ver video en Fig. D), hasta producir en el rayo rápido el retraso suficiente para igualarlo con el lento, en este momento observamos el grano de color gris. A continuación, quitamos la lámina del mineral y observamos el color que aparece en el centro del campo visual del microscopio. Este color está generado por la cuña de cuarzo y corresponde al retardo del mineral estudiado. En el caso de que al sacar la cuña de cuarzo el color observado se repita, tendremos un color de orden superior (2º o 3º orden). La birrefringencia se calcula con la tabla de Michel-Lévy.
En minerales fuertemente coloreados este color gris puede tener una dominante ya que al color de interferencia se le suma el color del mineral.
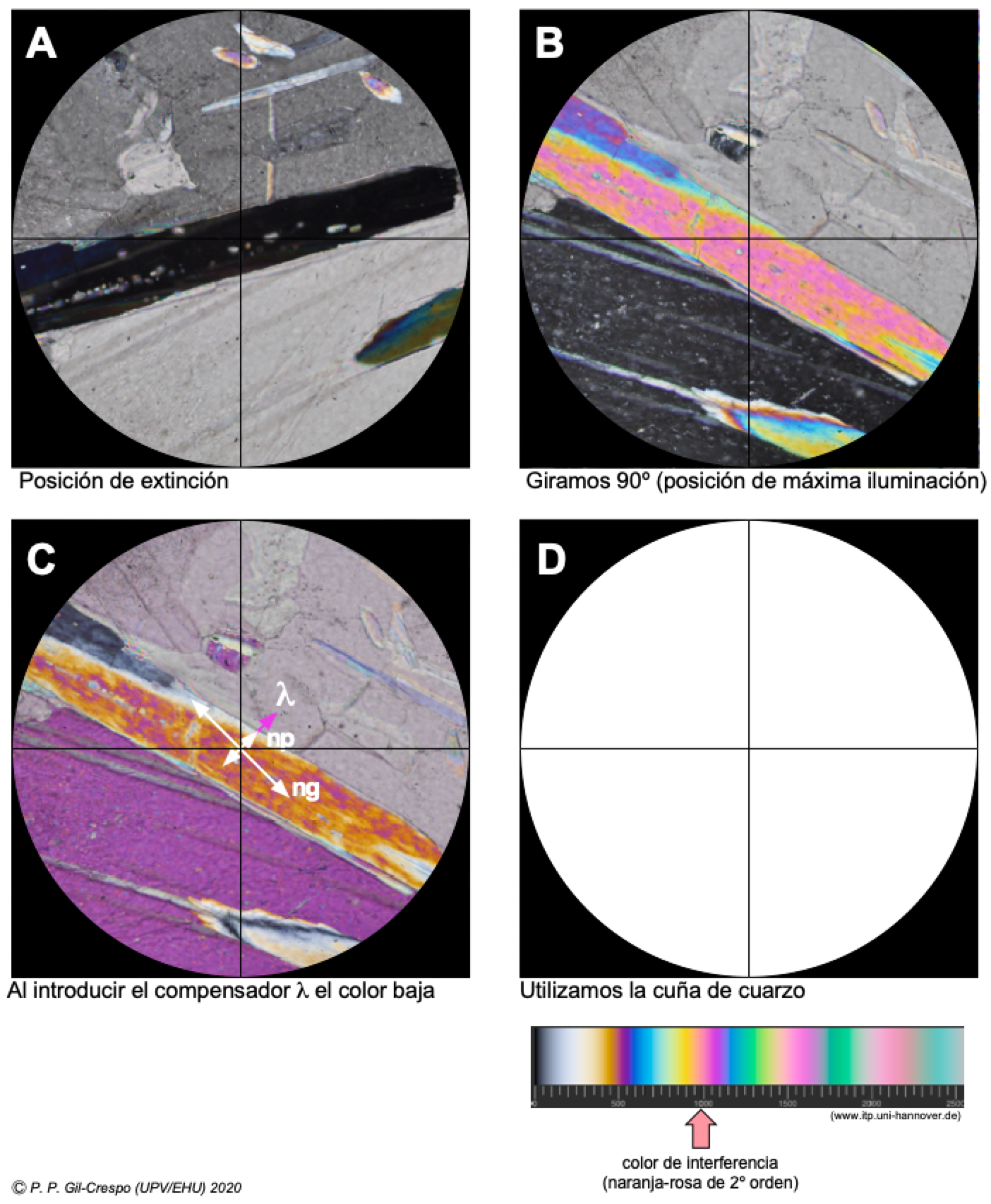
Identificación del color de interferencia utilizando la cuña de cuarzo. Partimos de la posición de extinción (A) y giramos 45 ª para encontrar el color de interferencia en la posición de máxima iluminación (B). Como al introducir el compensador λ el color baja (C), introducimos lentamente la cuña de cuarzo (D, vídeo en bucle) hasta encontrar un color gris. Retiramos la lámina delgada, e identificamos el color de interferencia obtenido. En este ejemplo, al extraer la cuña de cuarzo el color naranja-rosa se repite una vez, por lo que color que tenemos es de 2º orden.
DETERMINACIÓN DEL COLOR DE INTERFERENCIA MEDIANTE LAS BANDAS DE COLORES EN BORDES DE GRANO ACUÑADOS
En algunos casos favorables, es posible determinar el orden de un color de interferencia sin necesidad de utilizar compensadores. Esto se consigue fácilmente si el mineral se adelgaza, en alguno de sus bordes, en forma de cuña. En este borde acuñado se puede observar la escala de los colores de Newton en una secuencia, ascendente, desde el borde al centro del grano. Las bandas rojas son visibles y marcan el límite superior de cada orden. Supongamos que el color de interferencia de un grano es predominantemente verde (ver Fig. A) y dos bandas rojas se ven en el borde acuñado del fragmento. La banda roja más externa marca el límite superior de los colores de primer orden y la siguiente banda roja el límite de los colores de segundo orden. De acuerdo con esto, el verde debe de ser un color de tercer orden. En el segundo ejemplo (ver Fig. B) el color es el azul de 2º orden. Apartir de aquí, determinamos la birrefringencia con la tabla de Michel-Lévy.
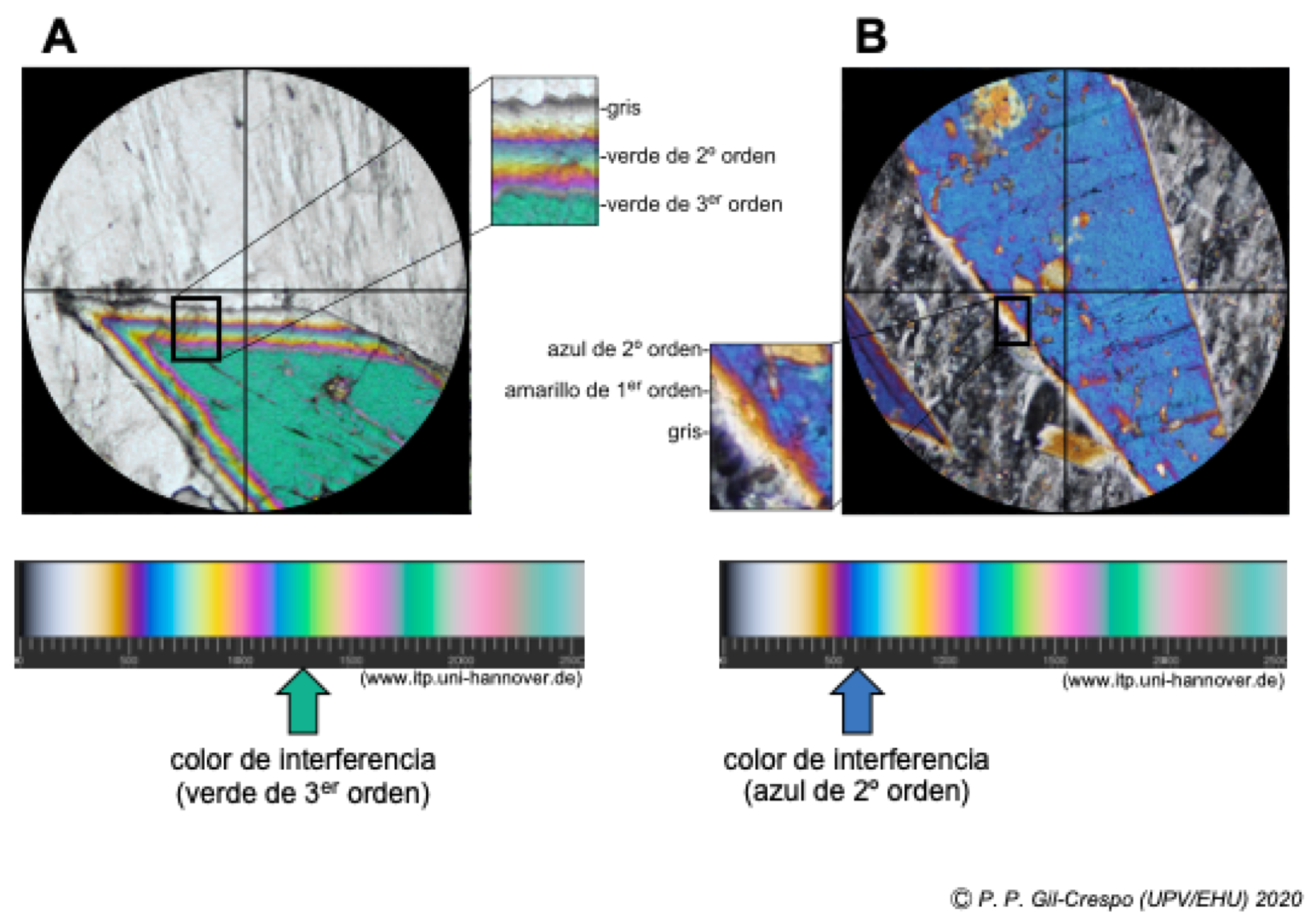
Identificación del color de interferencia los bordes de grano adelgazado. En A: el color de interferencia es el 2º verde, de tercer orden; en B: el color de interferencia es el primer azul, de 2º orden.
COLOR DE INTERFERENCIA; BIRREFRINGENCIA e INDICATRICES ÓPTICAS
Podemos representar todos los colores de interferencia posibles, para una indicatriz dada, mediante curvas de “iso-birrefringencia”. Para cada dirección de la indicatriz obtenemos el color de interferencia correspondiente al retardo de la luz que atraviesa la indicatriz en esa dirección y que corresponde a la birrefringencia de su sección perpendicular (ver ejemplos en la figura). En las indicatrices uniáxicas (A y B), los rayos que atraviesan el mineral en cualquier dirección perpendicular al eje óptico (ε) presentan el mayor retardo ya que las secciones perpendiculares a estas direcciones (ε - ω) son las de birrefringencia máxima. Los rayos que atraviesan el mineral en la dirección paralela al eje óptico, presentan un retardo igual a 0, ya que la birrefringencia de la sección perpendicular (ω-ω) también es igual a 0 y, por lo tanto, no se produce la doble refracción.
En las indicatrices biáxicas (C y D), la distribución de colores de interferencia es más compleja debido a que tenemos tres índices de refracción principales y dos ejes ópticos. En estos casos la sección de mayor birrefringencia y, por lo tanto de mayor retardo, es la que contiene a los dos ejes ópticos (plano óptico) y el mayor color de interferencia se observa en los rayos de luz que atraviesan el mineral perpendicularmente a esta sección. Las secciones de menor birrefringencia (retardo = 0) son las perpendiculares a los ejes ópticos.
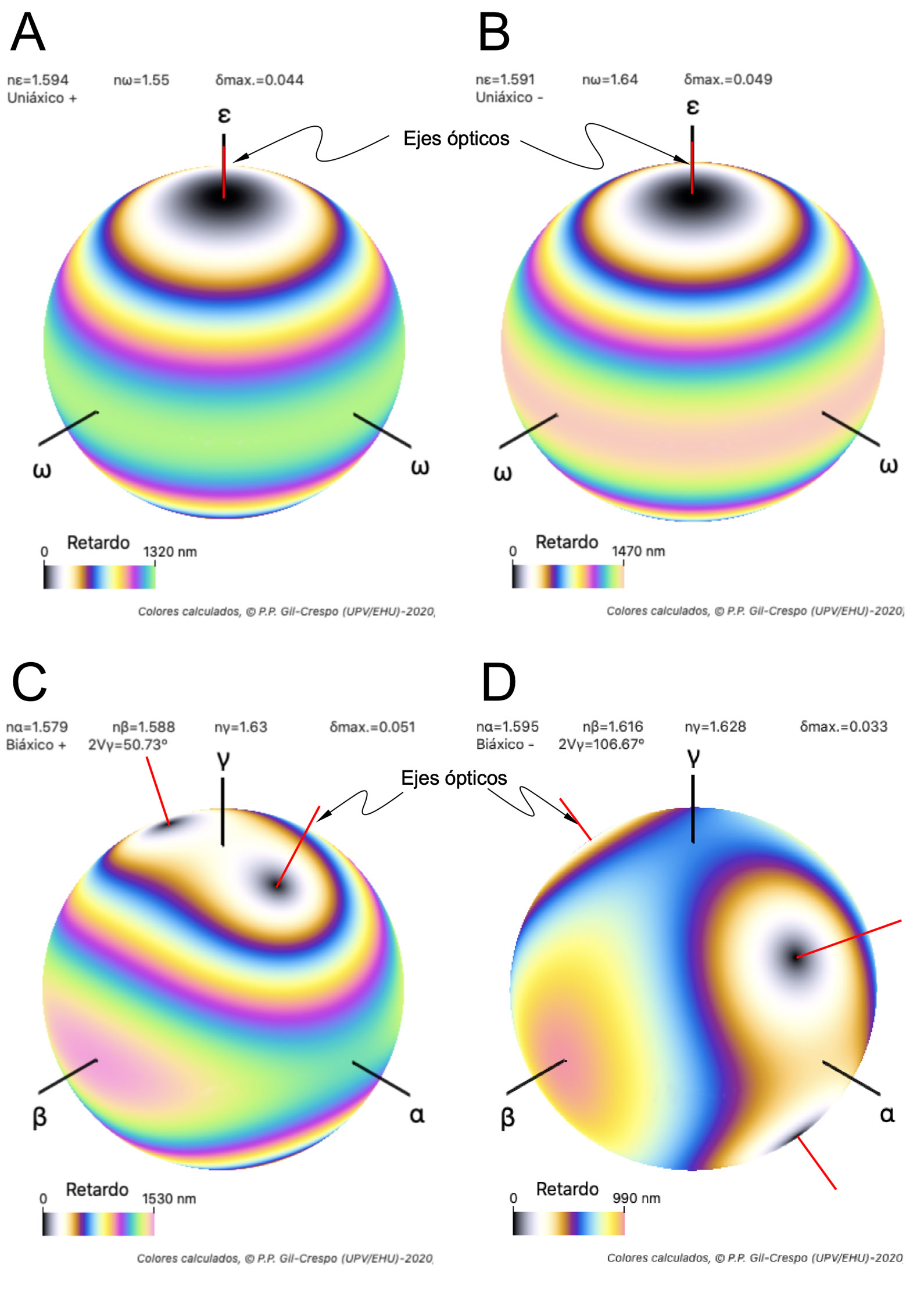
Ejemplos de curvas de “iso-birrefringencia” en indicatrices ópticas anisótropas: A = uniáxico positivo, B = uniáxico negativo, C = biáxico positivo y C = biáxico negativo. Colores de interferencia calculados para un espesor de 30 micras (δmax. = birrefringencia máxima).
Hay que recordar que el retardo (color de interferencia) de una sección concreta de un mineral depende de la birrefringencia, en la sección considerada, y del espesor de la muestra. Aunque el estándar de las láminas delgadas utilizadas en petrografía es de 30 micras, podemos tener muestras con grosores diferentes, lo que afectaría al color de interferencia observado. En la figura se muestra un ejemplo de la variación de los colores de interferencia en para tres espesores diferentes de un mismo mineral.
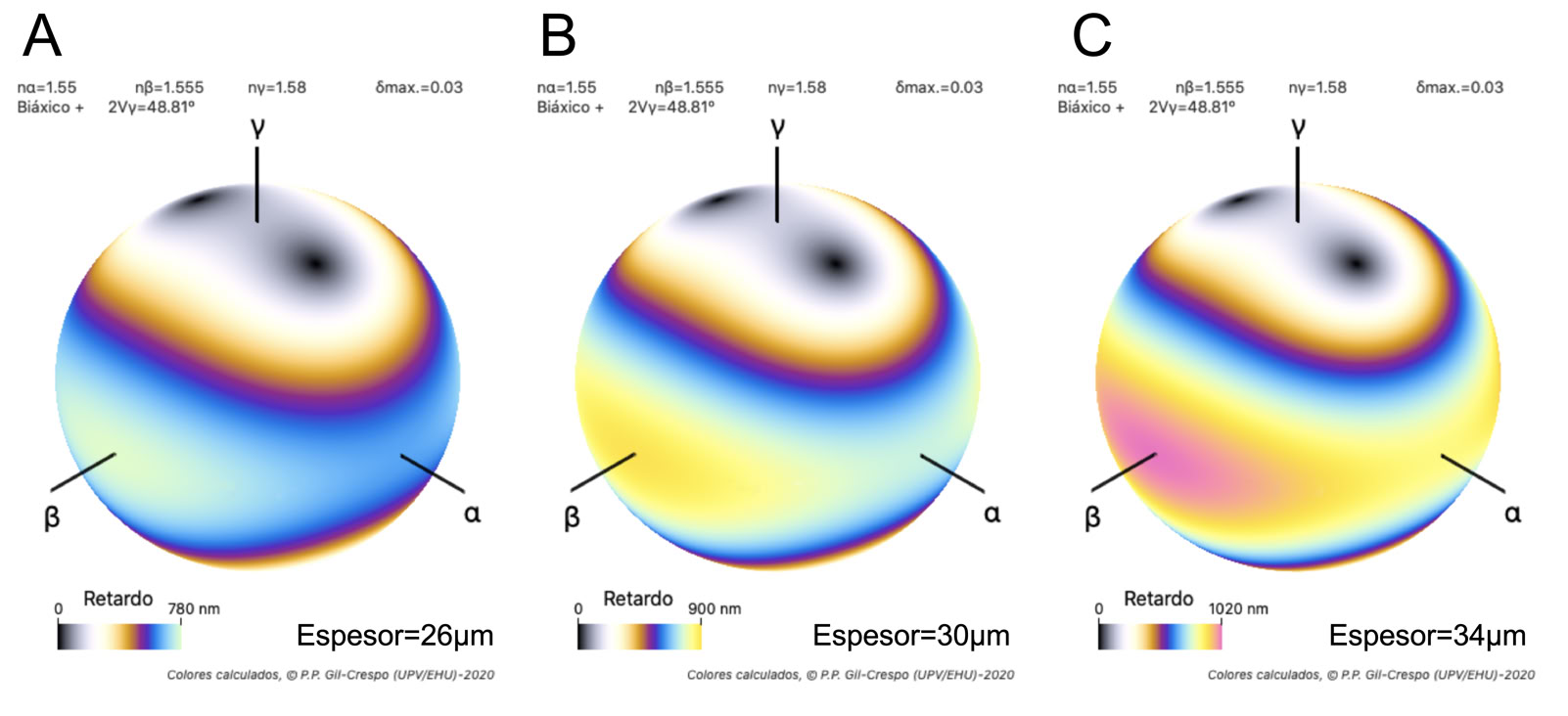
Ejemplos de variaciones del retardo (y del color de interferencia) para diferentes espesores del mismo mineral.
EJEMPLOS DE COLORES DE INTERFERENCIA EN LÁMINA DELGADA
Comportamiento de un mineral isótropo en el microscopio petrográfico. Permanece siempre en extinción al girar la muestra (ej. granate). Polarizadores cruzados.
Lado mayor de la imagen (mm)= 2.7
Comportamiento de un mineral anisótropo en el microscopio petrográfico. Presenta posiciones de extinción y de iluminación (colores de interferencia) al girar la muestra (ej. epidota). Polarizadores cruzados.
Lado mayor de la imagen (mm)= 2.5


Colores de inteferencia bajos, gris-blanco de primer orden (birrefringencia baja= 0.009) en cristales xenomorfos de cuarzo. Polarizadores cruzados.
Lado mayor de la imagen (mm)= 5
Colores de inteferencia rojos-azules del principio del 2º orden (birrefringencia media= 0.018-0.020) en cristales automorfos de hornblenda. Polarizadores cruzados.
Lado mayor de la imagen (mm)= 4.8


Colores de interferencia altos, hasta azul-verde de principio del tercer orden (birrefringencia alta = 0.037-0.042) en cristales de moscovita. Polarizadores cruzados.
Lado mayor de la imagen (mm)= 3.4
Colores de interferencia muy altos, de hasta finales de tercer orden, (birrefringencia muy alta, 0.050) en cristales de epidota. Polarizadores cruzados.
Lado mayor de la imagen (mm)= 6.5


Colores de interferencia de órdenes superiores, mayores del cuarto orden (birrefringencia extrema = 0.172) en cristales de calcita. Polarizadores cruzados.
Lado mayor de la imagen (mm)= 4
Colores de interferencia anómalos ultra-azules (no se corresponden con los de la tabla de Michel-Leví), en cristales de clorita (la birrefringencia es baja). Polarizadores cruzados.
Lado mayor de la imagen (mm)= 3